diff --git a/07/JiYongKim/DFS_BFS.md b/07/JiYongKim/DFS_BFS.md
new file mode 100644
index 00000000..173c940e
--- /dev/null
+++ b/07/JiYongKim/DFS_BFS.md
@@ -0,0 +1,427 @@
+**※ 그래프 탐색**
+
+- 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것
+
+Ex) 특정 도시에서 다른 도시로 갈 수 있는지 없는지, 전자 회로에서 특정 단자와 단자가 서로 연결되어 있는지
+
+
+
+**※ 깊이 우선 탐색 (DFS, Depth-First Search)의 개념**
+
+- 루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
+
+1. 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사함
+
+2. 즉 넓게(wide) 탐색하기 전에 깊게(deep) 탐색함
+
+**3. 모든 노드를 방문하고자 하는 경우에 이 방법을 선택함**
+
+4. 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단함
+
+5. 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느림
+
+
+
+**※ 깊이 우선 탐색(DFS)의 특징**
+
+- 자기 자신을 호출하는 순환 알고리즘의 형태를 지님
+- 이 알고리즘을 구현할 때 가장 큰 차이점은 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야한다는 것 (이를 검사하지 않을 경우 무한루프에 빠질 위험이 있음)
+
+
+
+**※ 깊이 우선 탐색(DFS)의 과정**
+
+
+
+
+
+
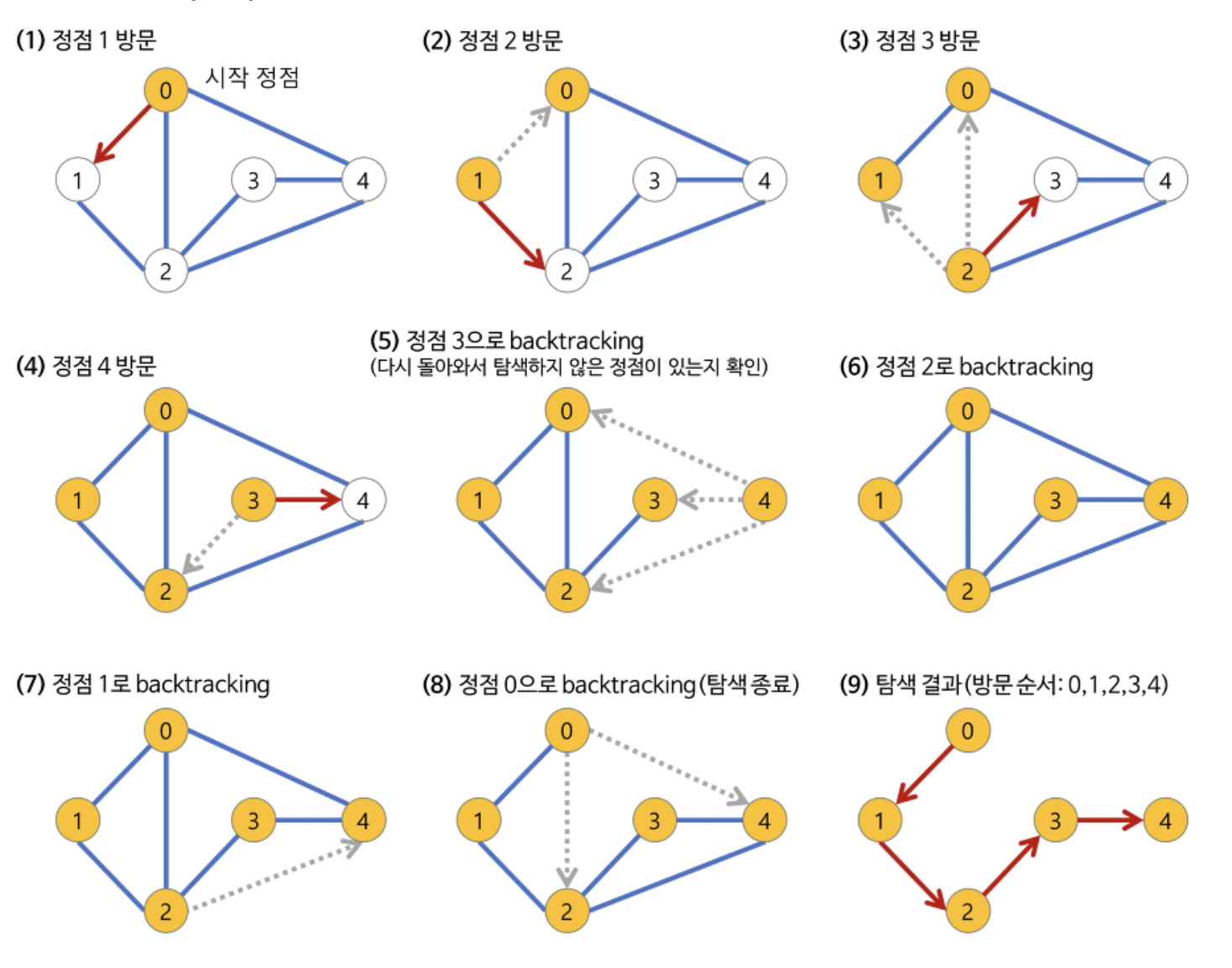+**※ 깊이 우선 탐색(DFS)의 시간 복잡도**
+
+- DFS는 그래프(정점의 수 : N, 간선의 수: E)의 모든 간선을 조회함
+- 인접 리스트로 표현된 그래프 : O(N+E)
+- 인접 행렬로 표현된 그래프 : O(N^2)
+
+
+
+* * *
+
+
+**※ 너비 우선 탐색 (BFS, Breadth-First Search)**
+
+- 루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법
+
+1. 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법
+
+2. 즉 깊게(deep) 탐색하기 전에 넓게(wide) 탐색하는 것
+
+3. **두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 선택함**
+
+ex) 지구 상에 존재하는 모든 친구 관계를 그래프로 표현한 후 Ash 와 Vanessa 사이에 존재하는 경로를 찾는 경우
+
+- 깊이 우선 탐색의 경우 - 모든 친구 관계를 다 살펴봐야할지도 모름
+- 너비 우선 탐색의 경우 - Ash와 가까운 관계부터 탐색
+
+
+
+**※ 너비 우선 탐색(BFS)의 특징**
+
+- BFS 는 재귀적으로 동작하지 않는다.
+- 이 알고리즘을 구현할 때 가장 큰 차이점은 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사해야한다는 것이다 이를 검사하지 않을 경우 무한 루프에 빠질 위험이 있다.
+- BFS 는 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 자료 구조인 큐(Queue)를 사용함
+- 즉 선입선출(FIFO) 원칙으로 탐색
+
+
+
+**※ 너비 우선 탐색(BFS)이 과정**
+
+- 깊이가 1인 모든 노드를 방문하고 나서 그 다음에는 깊이가 2인 모든 노드를, 그 다음에는 깊이가 3인 모든 노드를 방문하는 식으로 계속 방문하다가 더 이상 방문할 곳이 없으면 탐색을 마친다.
+
+
+
+
+
+
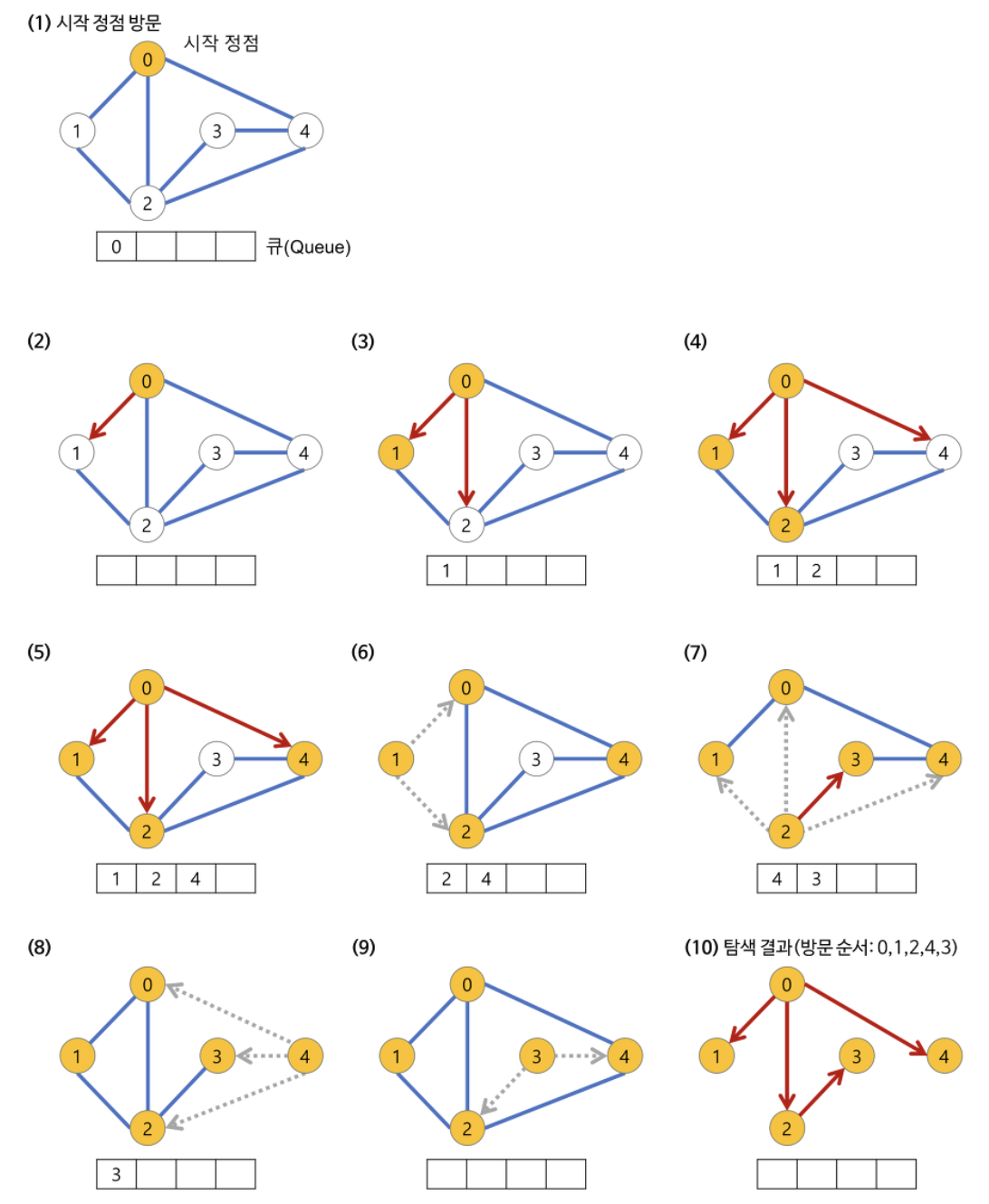+**※ DFS 와 BFS 의 차이**
+
+997C3C3E5BD01AF41D](https://t1.daumcdn.net/cfile/tistory/997C3C3E5BD01AF41D)
+
+
+
+* * *
+
+
+## 구현
+
+DFS 구현
+
+ DFS
+ ## DFS
+
+· DFS(**Depth-First Search**)는 **깊이 우선 탐색**이라고 부르며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘
+
+### 알고리즘 동작 방식
+
+· **스택 자료구조**를 이용한다.
+
+1. 탐색 시작 노드를 스택에 삽입하고, 방문 처리한다.
+
+2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문 처리하고,
+
+방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
+
+3. 위의 1번과 2번 과정을 더 이상 수행할 수 없을 때까지 반복한다.
+
+- ‘**방문 처리':** 스택에 한 번 삽입되어 처리된 노드가 다시 삽입되지 않게 체크하는 것을 의미한다. 이를 통해 각 노드를 한 번씩만 처리할 수 있다.
+
+▶ 예시 - 그래프의 노드 1을 시작 노드로 설정하여 DFS를 이용해 탐색
+
+
+
+인접한 노드 중에서 방문하지 않은 노드가 여러 개 있으면 번호가 낮은 순서부터 처리한다.
+
+방문 처리된 노드는 회색으로, 현재 처리하는 스택의 최상단 노드는 하늘색으로 표현한다.
+
+**step1.** 시작 노드 ‘1’을 스택에 삽입하고 방문 처리
+
+
+
+**step2.** 스택의 최상단 노드 ‘1’에 방문하지 않은 인접 노드 ‘2’, ‘3’, ‘8’ 중에서 가장 작은 노드 ‘2’를 스택에 넣고 방문 처리
+
+
+
+**step3.** 스택의 최상단 노드 ‘2’에 방문하지 않은 인접 노드 ‘7’을 스택에 넣고 방문 처리
+
+
+
+**step4.** 스택의 최상단 노드 ‘7’에 방문하지 않은 인접 노드 ‘6’과 ‘8’ 중에서 가장 작은 노드인 ‘6’을 스택에 넣고 방문 처리
+
+
+
+**step5.** 스택의 최상단 노드 ‘6’에 방문하지 않은 인접 노드가 없으므로, 스택에서 ‘6’번 노드를 꺼냄
+
+
+
+**step6.** 스택의 최상단 노드 ‘7’에 방문하지 않은 인접 노드 ‘8’이 있으므로, ‘8’번 노드를 스택에 넣고 방문 처리
+
+
+
+**step7.** 스택 최상단 노드 ‘8’에 방문하지 않은 인접 노드가 없으므로, 스택에서 ‘8’번 노드를 꺼냄
+
+
+
+**step8.** 스택의 최상단 노드 ‘7’에 방문하지 않은 인접 노드가 없으므로, 스택에서 ‘7’번 노드를 꺼냄
+
+
+
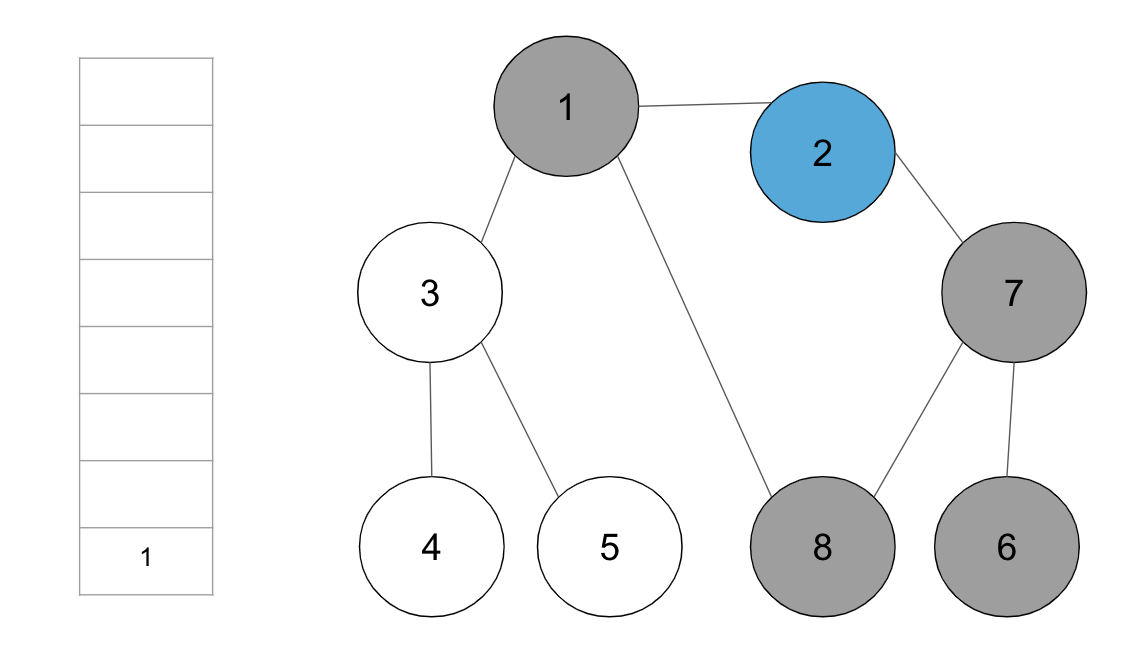
+**step9.** 스택의 최상단 노드 ‘2’에 방문하지 않은 인접 노드가 없으므로, 스택에서 ‘2’번 노드를 꺼냄
+
+
+
+**step10.** 스택의 최상단 노드 ‘1’에 방문하지 않은 인접 노드 ‘3’을 스택에 넣고 방문 처리
+
+
+
+**step11.** 스택의 최상단 노드 ‘3’에 방문하지 않은 인접 노드 ‘4’, ‘5’ 중 가장 작은 노드 ‘4’를 스택에 넣고 방문 처리
+
+
+
+**step12.** 스택의 최상단 노드 ‘4’에 방문하지 않은 인접 노드 ‘5’가 있으므로, ‘5’번 노드를 스택에 넣고 방문 처리
+
+
+
+**step13.** 남아 있는 노드에 방문하지 않은 인접 노드가 없다. 따라서 모든 노드를 차례대로 꺼내면 다음과 같다.
+
+
+
+위 단계에서 노드의 탐색 순서(스택에 들어간 순서)는 다음과 같다.
+
+1 -> 2 -> 7 -> 6 -> 8 -> 3 -> 4 -> 5
+
+**·** 깊이 우선 탐색 알고리즘인 DFS는 **스택 자료구조**에 기초하므로, 실제 구현은 **재귀 함수**를 이용했을 때 간결하게 구현할 수 있다.
+
+**· 소요시간:** 데이터의 개수가 N개인 경우, O(N)
+
+▶ 예시 - 재귀 함수를 통해 dfs 구현
+
+```java
+public class DFSExamRecursion {
+//각 노드가 방문된 정보를 1차원 배열 자료형으로 표현public static boolean [] visited = {false, false, false ,false ,false ,false ,false ,false, false};
+// 각 노드가 연결된 정보를 2차원 배열 자료형으로 표현public static int[][] graph = {{},
+ {2, 3, 8},
+ {1, 7},
+ {1, 4, 5},
+ {3, 5},
+ {3, 4},
+ {7},
+ {2, 6, 8},
+ {1, 7}};
+
+ public static void main(String[] args){
+ int start = 1;// 시작 노드
+ dfs(start);
+ }
+
+/*
+ * dfs 알고리즘을 수행하는 함수
+ * @param v 탐색할 노드
+ */public static void dfs(int v){
+// 현재 노드 방문 처리
+ visited[v] = true;
+// 방문 노드 출력
+ System.out.print(v + "");
+
+// 인접 노드 탐색for (int i : graph[v]){
+// 방문하지 않은 인접 노드 중 가장 작은 노드를 스택에 넣기if (visited[i]==false){
+ dfs(i);
+ }
+ }
+ }
+}
+```
+
+
+
+DFSExam 결과
+
+예시 - Stack 클래스를 통한 DFS 구현
+
+```sql
+public class DFS_Stack {
+ public static void main(String[] args){
+
+ //각 노드가 연결된 정보를 2차원 배열 자료형으로 표현
+ int [][]graph = {{},
+ {2, 3, 8},
+ {1, 7},
+ {1, 4, 5},
+ {3, 5},
+ {3, 4},
+ {7},
+ {2, 6, 8},
+ {1, 7}};
+
+ //각 노드가 방문된 정보를 1차원 배열 자료형으로 표현
+ boolean [] visited = {false, false, false ,false ,false ,false ,false ,false, false};
+
+ //정의된 DFS 함수 호출
+ DFS_Stack dfsExam = new DFS_Stack();
+ dfsExam.dfs(graph, 1, visited);
+ }
+
+/*
+ * dfs 메서드
+ * graph 노드 연결 정보를 저장
+ * v 방문을 시작하는 최상단 노드의 위치
+ * visited 노드 방문 정보를 저장
+ */
+ void dfs(int [][]graph,int start, boolean [] visited){
+ //시작 노드를 방문 처리
+ visited[start] = true;
+ System.out.print(start + " ");//방문 노드 출력
+
+ Deque stack = new LinkedList<>();
+ stack.push(start); //시작 노드를 스택에 입력
+
+ while(!stack.isEmpty()){
+ int now = stack.peek();
+
+ boolean hasNearNode = false; // 방문하지 않은 인접 노드가 있는지 확인
+ //인접한 노드를 방문하지 않았을 경우 스택에 넣고 방문처리
+ for(int i: graph[now]){
+ if (!visited[i]) {
+ hasNearNode = true;
+ stack.push(i);
+ visited[i] = true;
+ System.out.print(i + " ");//방문 노드 출력
+ break;
+ }
+ }
+ //반문하지 않은 인접 노드가 없는 경우 해당 노드 꺼내기
+ if(hasNearNode==false)
+ stack.pop();
+ }
+ }
+ }
+```
+
+
+BFS 구현
+
+ BFS
+ **·** BFS(Breadth First Search)의 약자로 ‘**너비 우선 탐색**’ 알고리즘을 의미한다.
+
+- 즉, **가까운 노드부터 탐색**하는 알고리즘이다.
+
+- 최대한 멀리 있는 노드를 우선으로 탐색하는 DFS와는 반대다.
+
+### 알고리즘의 동작 방식
+
+**·** 선입선출 방식인 **큐** 자료구조를 이용하는 것이 정석이다.
+
+**- 인접한 노드를 반복적으로 큐에 넣도록 알고리즘을 작성**하면 자연스럽게 먼저 들어온 것이 먼저 나가며, 가까운 노드부터 탐색하게 된다.
+
+1. 탐색 시작 노드를 큐에 삽입하고 방문 처리한다.
+
+2. 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리한다.
+
+3. 위의 1번과 2번 과정을 더 이상 수행할 수 없을 때까지 반복한다.
+
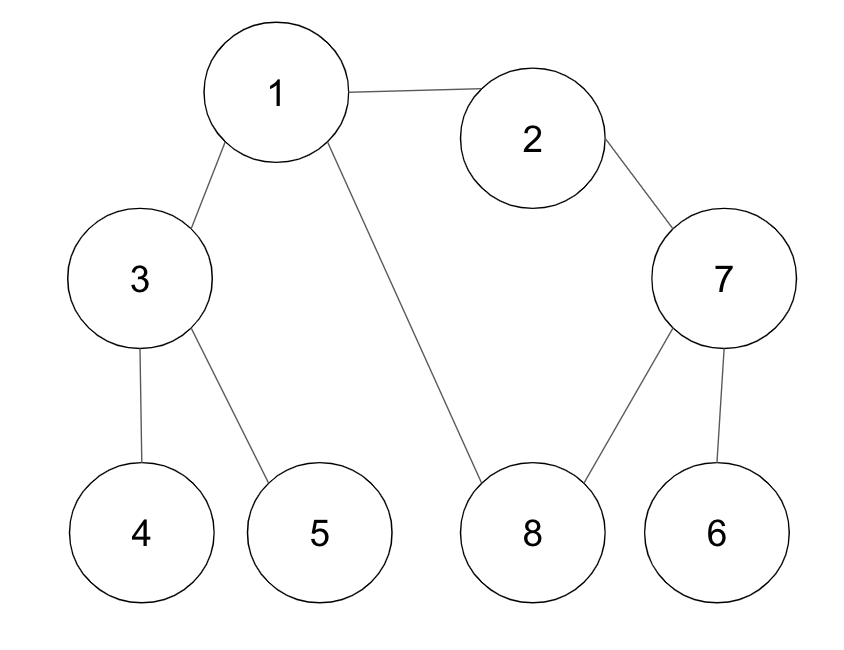
+**▶ 예시 - 그래프의 노드 1을 시작 노드로 설정하여 BFS를 이용해 탐색**
+
+**·** 인접한 노드가 여러 개 있을 때, 숫자가 작은 노드부터 먼저 큐에 삽입한다고 가정한다.
+
+큐에 원소가 들어올 때, 위에서 들어오고 아래쪽에서 꺼낸다.
+
+
+
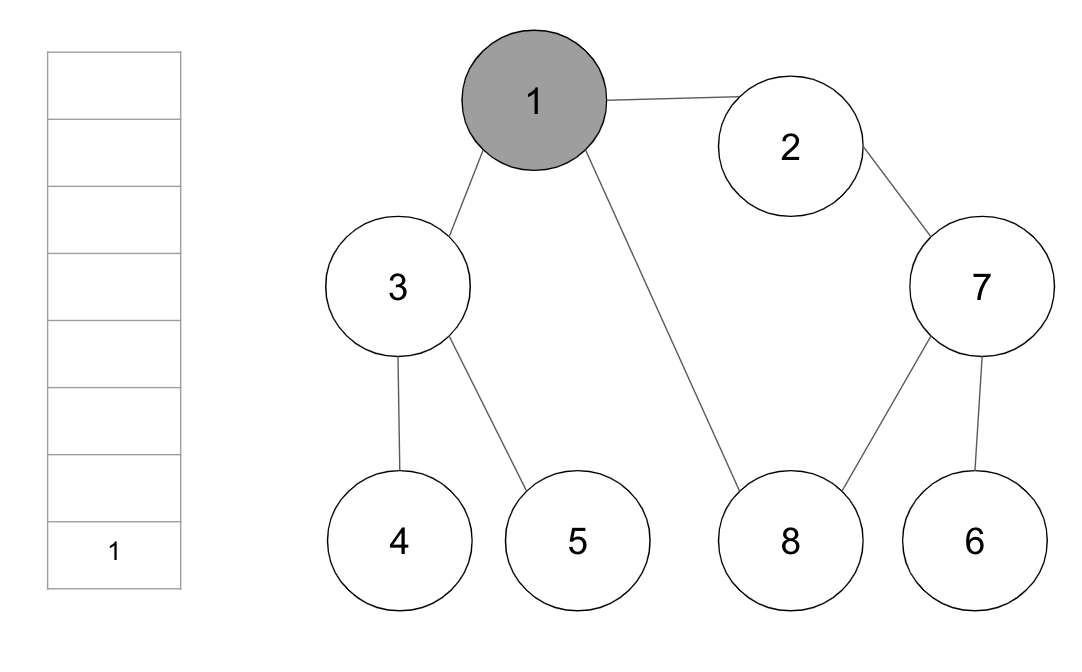
+**step 1.** 시작 노드 ‘1’을 큐에 삽입하고 방문 처리 한다.
+
+방문 처리된 노드는 회색으로, 큐에서 꺼내 현재 처리하는 노드는 하늘색으로 표시하다.
+
+
+
+**step 2.** 큐에서 노드 ‘1’을 꺼내고 방문하지 않은 인접 노드 ‘2’, ‘3’, ‘8’을 모두 큐에 삽입하고 방문 처리한다.
+
+
+
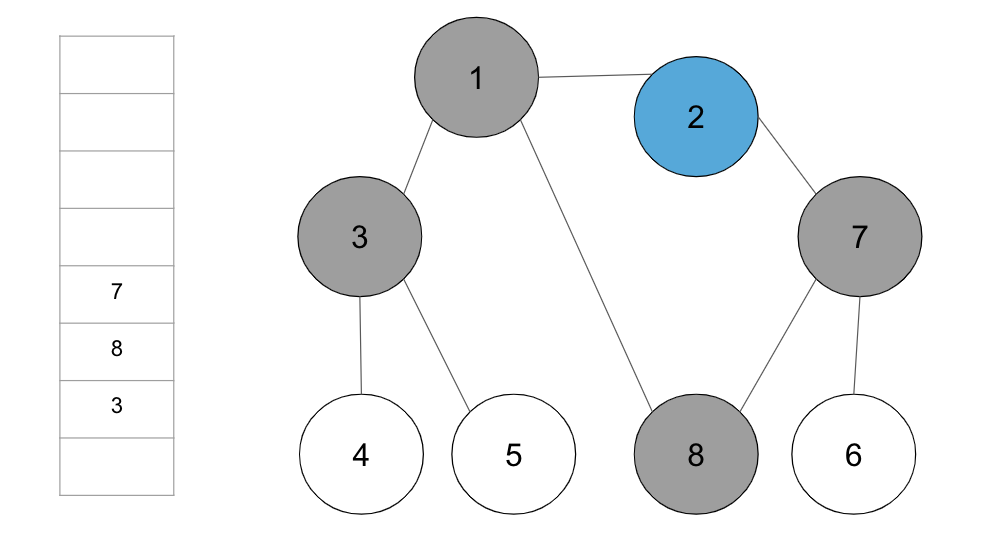
+**step 3.** 큐에서 노드 ‘2’를 꺼내고 방문하지 않은 인접 노드 ‘7’을 큐에 삽입하고 방문 처리 한다.
+
+
+
+**step 4.** 큐에서 노드 ‘3’을 꺼내고 방문하지 않은 인접 노드 ‘4’와 ‘5’를 모두 큐에 삽입하고 방문 처리한다.
+
+
+
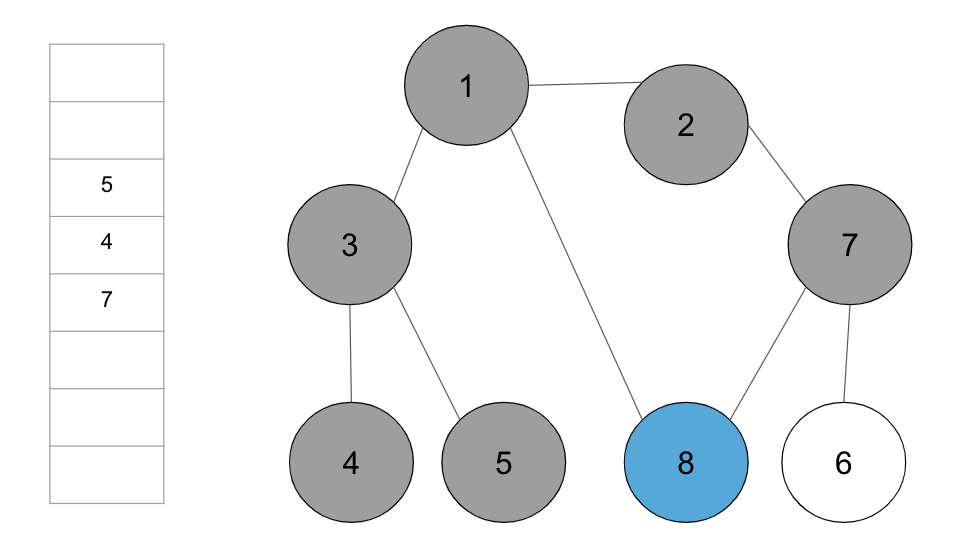
+step 5. 큐에서 노드 ‘8’을 꺼내고 방문하지 않은 인접 노드가 없으므로 무시한다.
+
+
+
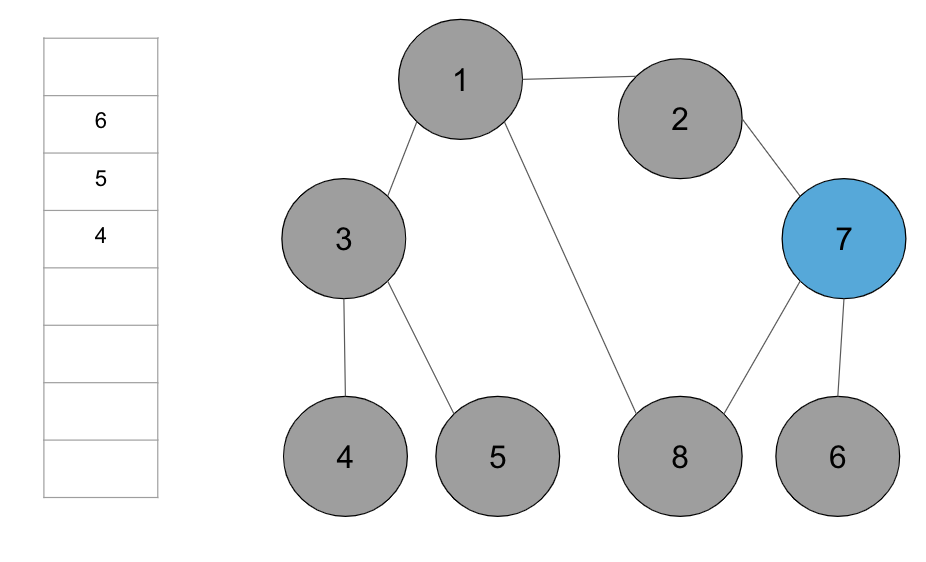
+**step 6.** 큐에서 노드 ‘7’을 꺼내고 방문하지 않은 인접 노드 ‘6’을 큐에 삽입하고 방문 처리를 한다.
+
+
+
+**step 7.** 남아 있는 노드에 방문하지 않은 인접 노드가 없다. 따라서 모든 노드를 차례로 꺼낸다.
+
+
+
+**노드의 탐색 순서**(큐에 들어간 순서) 1 -> 2 -> 3 -> 8 -> 7 -> 4 -> 5 -> 6
+
+**·** 너비 우선 탐색 알고리즘인 BFS는 **큐 자료구조**에 기초한다.
+
+**·** 구현할 때는 언어에서 제공하는 **큐 라이브러리**를 사용하자.
+
+**·** 탐색 수행 시간은 O(N)의 시간이 소요되고, 일반적인 경우 실제 **수행 시간**은 DFS보다 좋다.
+
+**-** 재귀 함수로 DFS를 구현하면 컴퓨터 시스템의 동작 특성상 실제 프로그램의 수행 시간이 느려질 수 있기 때문이다.
+
+```java
+import java.util.LinkedList;
+import java.util.Queue;
+
+public class BFS {
+ public static void main(String[] args){
+//각 노드가 연결된 정보를 2차원 배열 자료형으로 표현int [][]graph = {{},
+ {2, 3, 8},
+ {1, 7},
+ {1, 4, 5},
+ {3, 5},
+ {3, 4},
+ {7},
+ {2, 6, 8},
+ {1, 7}};
+
+//각 노드가 방문된 정보를 1차원 배열 자료형으로 표현boolean [] visited = {false, false, false ,false ,false ,false ,false ,false, false};
+
+ int start = 1;// 시작 노드// 큐 구현
+ Queue queue = new LinkedList<>();
+ queue.add(start);
+
+// 현재 노드를 방문 처리
+ visited[start] = true;
+
+// 큐가 빌때까지 반복while(!queue.isEmpty()){
+// 큐에서 하나의 원소를 뽑아 출력int v = queue.poll();
+ System.out.println(v + " ");
+
+// 인접한 노드 중 아직 방문하지 않은 원소들을 큐에 삽입for (int i : graph[v]){
+ if (visited[i] == false){
+ queue.add(i);
+ visited[i] = true;
+ }
+ }
+ }
+ }
+ }
+```
+
+**결과**
+
+
+
+
+
+
+
+* * *
+
+
+
+## 정리
+
+| | DFS | BFS |
+| --- | --- | --- |
+| 동작 원리 | 스택 | 큐 |
+| 구현 | 재귀 함수 또는 스택 자료구조 이용 | 큐 자료구조 이용 |
+
+**·** 앞서 DFS와 BFS를 설명하는 데 전형적인 그래프 그림을 이용했다.
+
+**1차원 배열**이나 **2차원 배열** 또한 **그래프 형태로 생각**하면 수월하게 문제를 풀 수 있다.
+
+**·** 예를 들어 게임 맵이 3 x 3 형태의 2차원 배열이고 각 데이터를 좌표라고 생각해보자.
+
+이때 각 표로 상하좌우로만 이동할 수 있다면, 모든 좌표의 형태를 다음처럼 그래프의 형태로 바꿔서 생각할 수 있다.
+
+
+
+**·** 코딩 테스트 중 2차원 배열에서의 탐색 문제를 만나면 이렇게 그래프 형태로 바꿔서 생각하자. 풀이 방법을 더 쉽게 떠올릴 수 있다.
diff --git a/07/JiYongKim/Graph.md b/07/JiYongKim/Graph.md
new file mode 100644
index 00000000..ff910a48
--- /dev/null
+++ b/07/JiYongKim/Graph.md
@@ -0,0 +1,95 @@
+## 그래프란?
+
+그래프란 ,수학자 오일러가 만든 “그래프 이론” 의 개념을 기초로 구성된 자료구조
+
+## 그래프의 용어
+
+
+
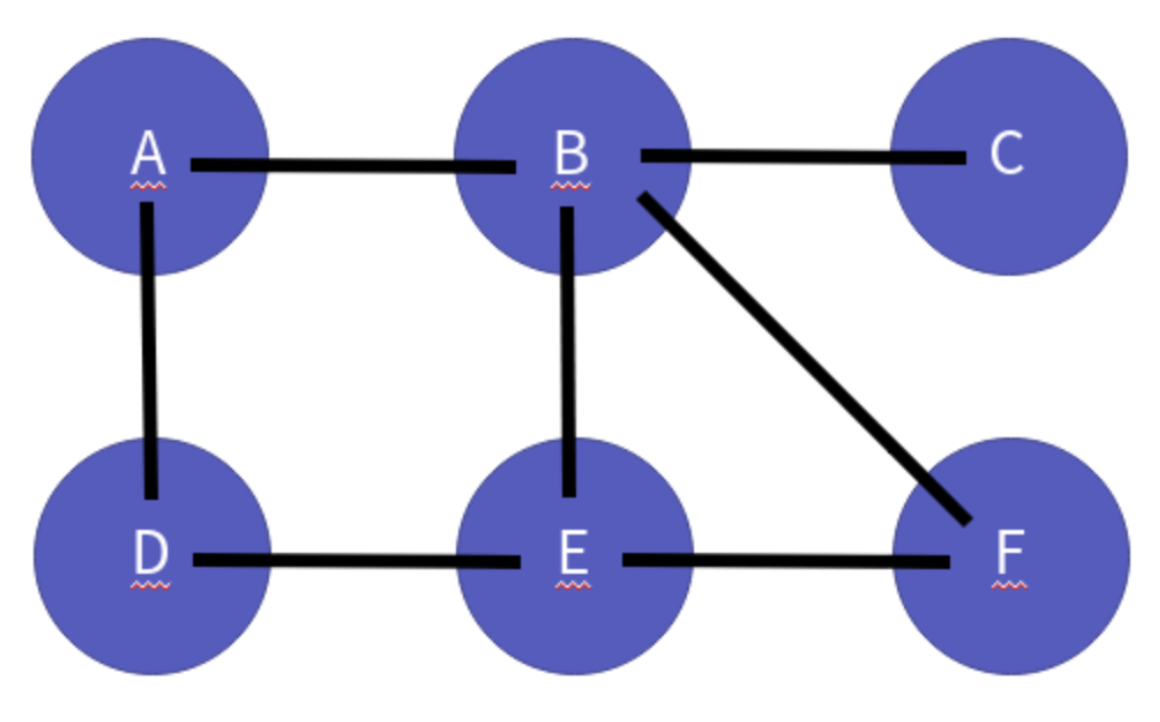+- 파란색 동그라미 : 정점 ( Vertex )
+- 검정색 실선 : 간선 ( Edge )
+
+## 그래프의 종류
+
+- 방향 그래프
+
+ 
+
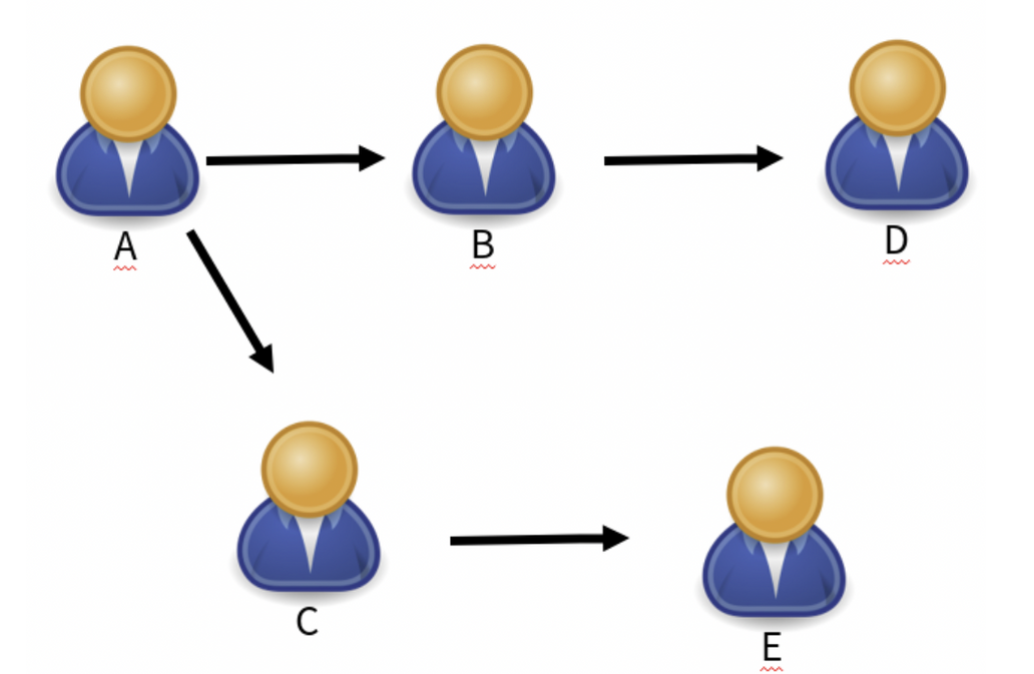+ - 방향 그래프는 간선의 방향이 존재하는 그래프
+ - ex)
+ - SNS 팔로우
+ - 5명의 유저 팔로우 관계에서 A → B → D 관계로 팔로우 하고 있다
+
+ ⇒ A는 B를 통해 D를 건너 볼 수 있다.
+
+
+ 즉 방향 그래프는 간선이 추가되면
+
+ - 한쪽 정점에서 다른 정점으로 이동은 가능 (A → B)
+ - 하지만 반대로의 이동은 불가능 ( B → A)
+
+- 무방향 그래프
+
+ 
+
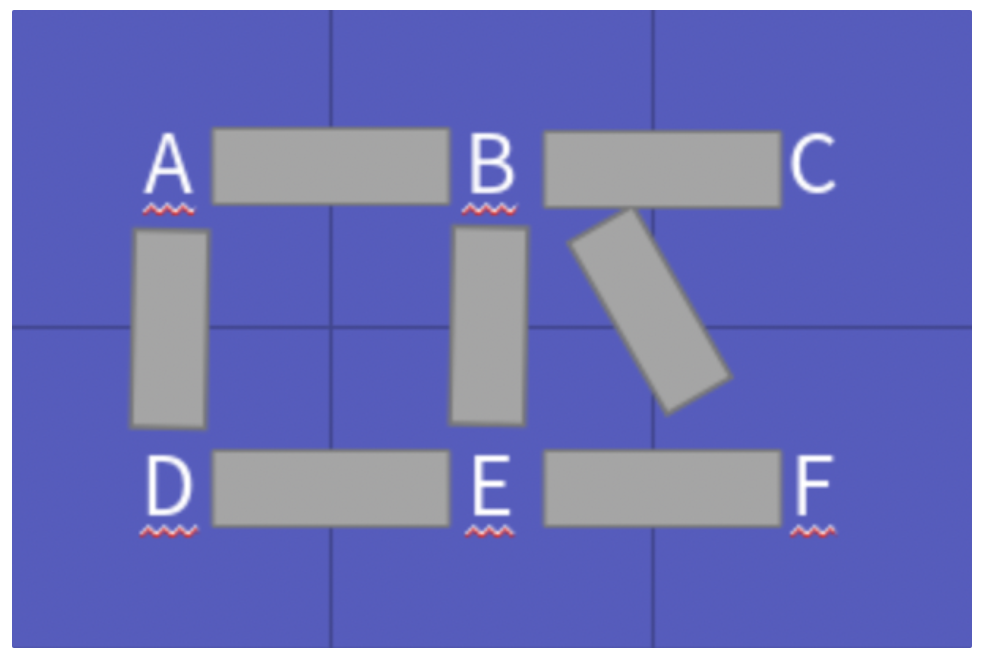+ - 무방향 그래프는 간선의 방향이 없어 서로간 왕복이 가능한 그래프
+
+
+## 그래프의 구현 방식
+
+그래프의 구현 방식에는 2가지 방식으로 나뉜다.
+
+- 인접 리스트 기반 그래프
+ - 인접 리스트 기반 그래프는 연결 리스트 배열을 만들고 다음과 같이 표현한다.
+
+ 
+
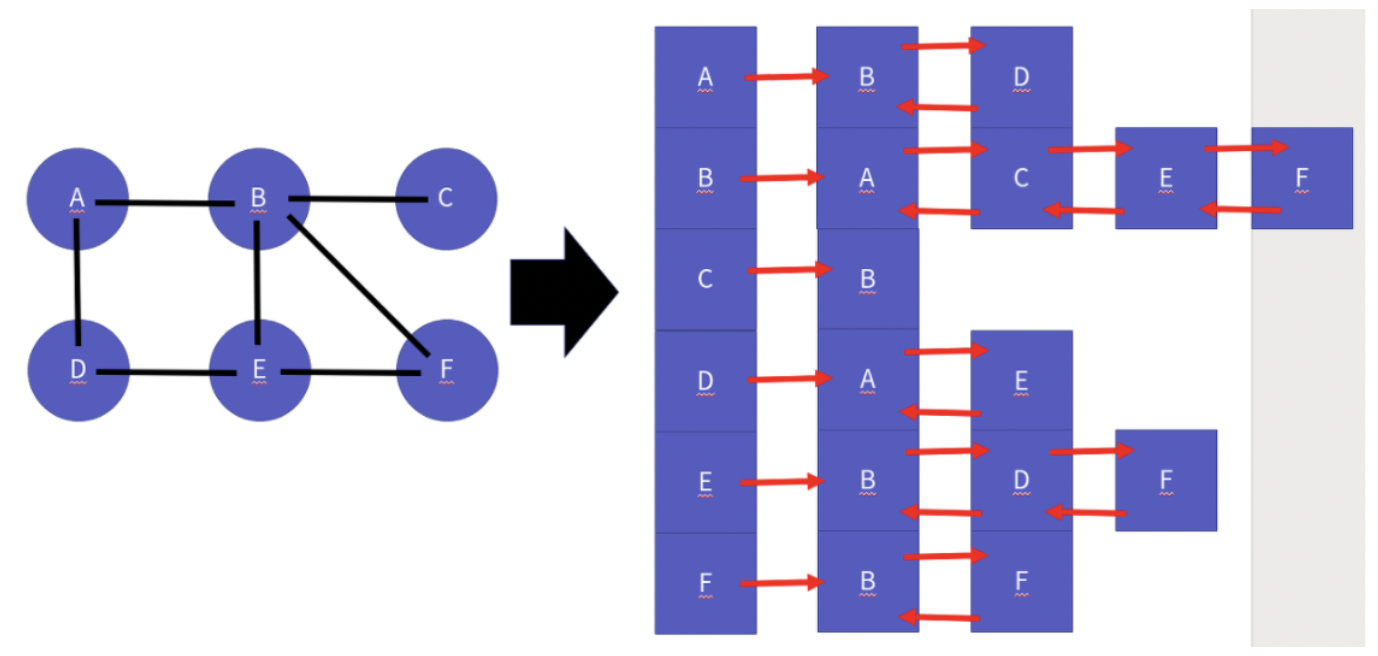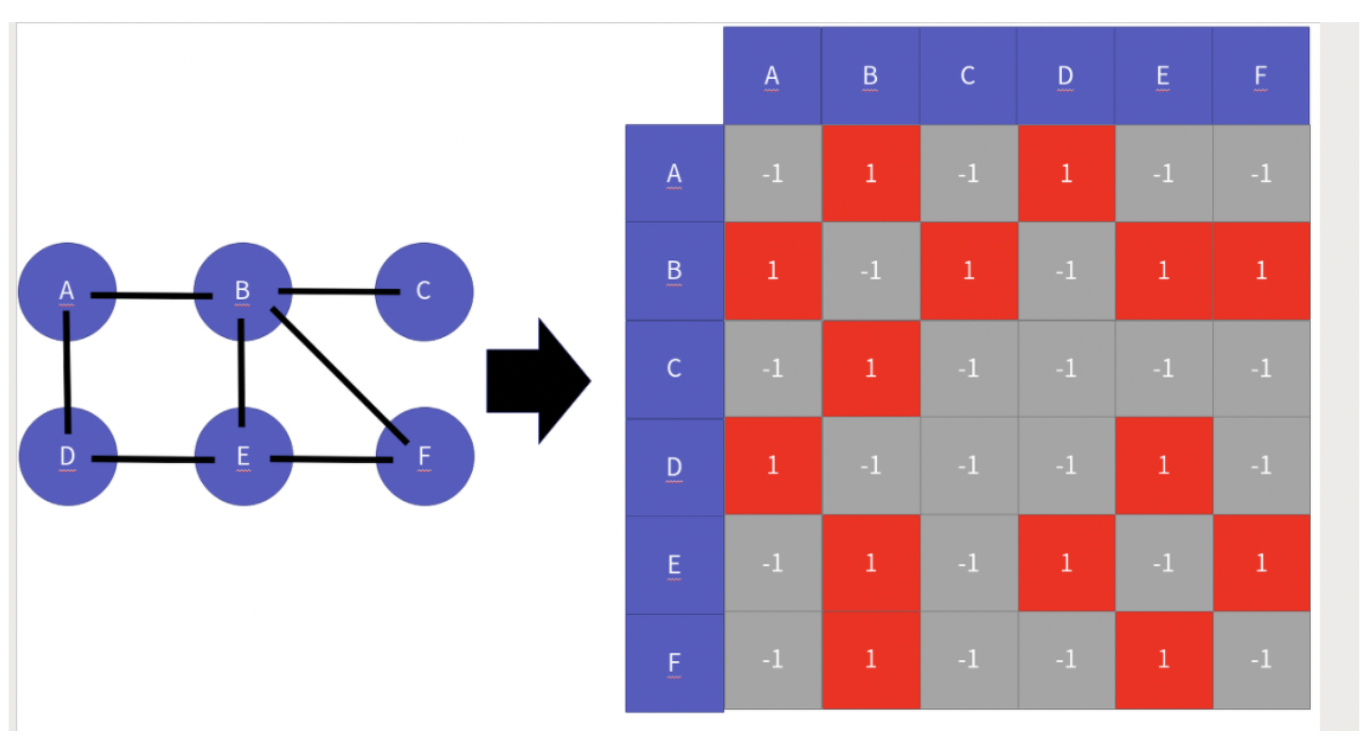
+- 인접 행렬 기반 그래프
+ - 인접 행렬 기반 그래프는 이차원 배열을 만들고
+ - 연결된 곳은 1
+ - 연결되지 않은 곳은 -1
+
+ ⇒ 같이 표현한다.
+
+
+ 
+
+
+즉 그래프를 가지고 위의 2가지 방식으로 표현이 가능하다.
+
+### 번외)
+
+
+### ADT(Abstract Data Type) 란??
+
+ADT의 정의 : **순수하게 기능이 무엇인지를 나열한 것을 가리켜 '추상 자료형' 혹은 ADT라고 한다.**
+
+### ADT의 사용 사례
+
+C언어
+
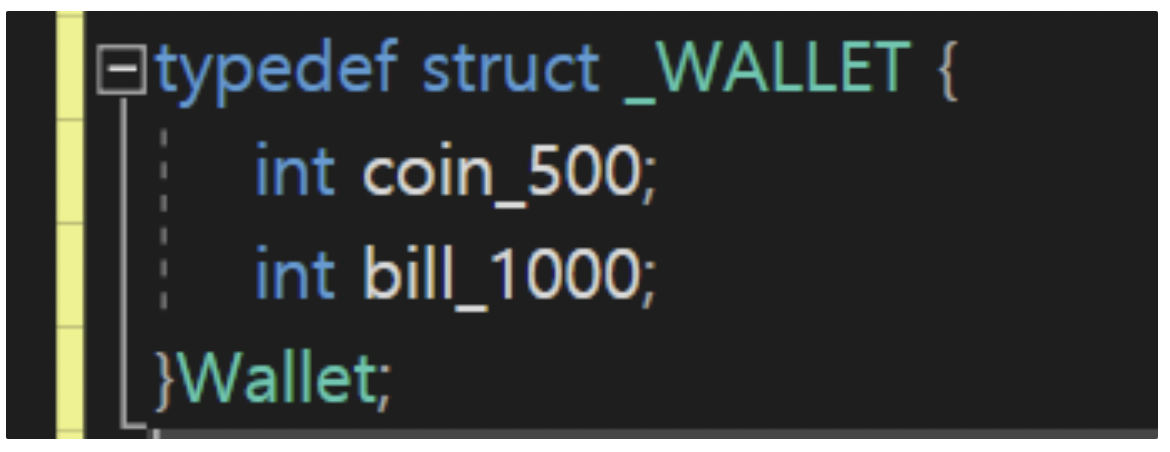
+- 구조체를 통해 사용자 정의 자료형이 정의된다. 지갑의 예를 들어보자.
+
+
+ 
+
+
+- 위의 구조체 정의를 통해 Wallet 자료형을 정의하고 속성으로 500원 동전, 1000원 지폐가 몇 개 담겨 있느냐를 표현하였다.(그러나 Wallet자료형에는 돈을 빼는 것, 돈을 넣는 것 이라는 기능이 있을 수 있다.)
+
+
+ 
+
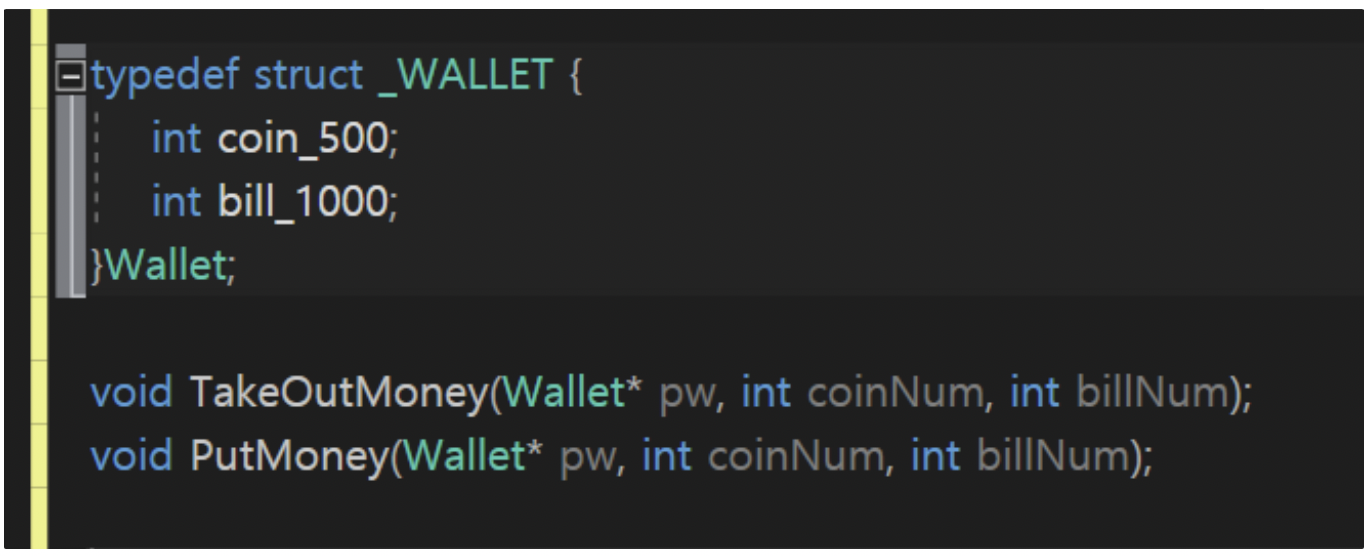+ ⇒ 이 기능들을 담고 있는 함수가 구조체 아래의 두 함수이다.
+
+
+**결론)**
+
+자료구조(연결리스트, 스택, 큐 등)의 ADT는
+
+- data를 담을 저장소를 만드는 것과
+- data를 다루는 함수들을 정의하는 것을
+
+ ⇒ 포함하는 개념인 것이다.
+
+
+**즉, 특정 자료형과 그 자료형을 바탕으로 하는 기능들(함수들)의 집합을 ADT라고 하는 것!**
diff --git a/07/JiYongKim/Graph.pptx b/07/JiYongKim/Graph.pptx
new file mode 100644
index 00000000..f22751cf
Binary files /dev/null and b/07/JiYongKim/Graph.pptx differ
diff --git a/07/JiYongKim/Leetcode.md b/07/JiYongKim/Leetcode.md
new file mode 100644
index 00000000..68c28953
--- /dev/null
+++ b/07/JiYongKim/Leetcode.md
@@ -0,0 +1,84 @@
+
+
+Graph 태그가 있는 문제들
+
+ 1791. Find Center of Star Graph
+- 1791. Find Center of Star Graph
+
+```java
+// 시간 복잡도 O(1)
+// 공간 복잡도 O(1)
+class Solution {
+ public int findCenter(int[][] edges) {
+
+
+ int a1 = edges[0][0];
+ int a2 = edges[0][1];
+
+ int b1 = edges[1][0];
+ int b2 = edges[1][1];
+
+ if(a1 == b1 || a1 == b2)
+ return a1;
+
+ else
+ return a2;
+ }
+}
+```
+
+
+
+
+
+ 997 . Find the Town Judge
+- 997 . Find the Town Judge
+
+```java
+// 시간 복잡도 O(a+b) .. a = trust의 크기, b = n
+// 공간 복잡도 O(a) ... a = n+1
+class Solution {
+ public int findJudge(int n, int[][] trust) {
+ int[] count = new int[n + 1];
+ for (int[] t : trust) {
+ count[t[0]]--;
+ count[t[1]]++;
+ }
+ for (int i = 1; i <= n; i++) {
+ if (count[i] == n - 1) {
+ return i;
+ }
+ }
+ return -1;
+ }
+}
+```
+
+
+
+
+
+ 1971. Find if Path Exists in Graph (미완)
+- 1971. Find if Path Exists in Graph
+
+
+
+
+
+Graph 순회 `알고리즘` + `사용해본 자료구조`
+
+
+ 653. Two Sum IV - Input is a BST (미완)
+- 653. Two Sum IV - Input is a BST
+
+
+
+
+
+
+ 463. Island Perimeter (미완)
+- 463. Island Perimeter
+
+
+
+
\ No newline at end of file
diff --git a/ADT/JiYongKim/Graph/ArrGraph.java b/ADT/JiYongKim/Graph/ArrGraph.java
new file mode 100644
index 00000000..c6d0f5e2
--- /dev/null
+++ b/ADT/JiYongKim/Graph/ArrGraph.java
@@ -0,0 +1,36 @@
+package ADT.JiYongKim.Graph;
+
+// 그래프(행렬) 클래스
+class ArrGraph {
+ private int[][] arrGraph;
+
+ // 그래프 초기화
+ public ArrGraph(int initSize) {
+ this.arrGraph = new int[initSize+1][initSize+1];
+ }
+
+ // 그래프 return
+ public int[][] getGraph() {
+ return this.arrGraph;
+ }
+
+ // 그래프 추가 (양방향)
+ public void insertVertexEdge(int x, int y) {
+ arrGraph[x][y] = arrGraph[y][x] = 1;
+ }
+
+ // 그래프 추가 (단방향)
+ public void putVertexEdge(int x, int y) {
+ arrGraph[x][y] = 1;
+ }
+
+ // 그래프 출력 (인접행렬)
+ public void printGraph() {
+ for(int i=0; i> listGraph;
+
+
+ public ListGraph(int initSize) {
+ this.listGraph = new ArrayList>(); // 그래프 생성
+
+ for(int i=0; i());
+ }
+ }
+
+ public ArrayList> getGraph() {
+ return this.listGraph;
+ }
+
+
+ public ArrayList getNode(int i) {
+ return this.listGraph.get(i);
+ }
+
+ // 그래프 정점 및 양방향 간선 추가
+ public void insertVertexEdge(int x, int y) {
+ listGraph.get(x).add(y);
+ listGraph.get(y).add(x);
+ }
+
+ // 그래프 정점 및 단방향 간선 추가
+ public void putVertexEdge(int x, int y) {
+ listGraph.get(x).add(y);
+ }
+
\ No newline at end of file